Last December I (Mr. Reynolds - KM) promised you an up-date on Cube Loading "in a couple months." So, I'm a little late. A lot late?

     For newcomers to the column, and as a review for "oldcomers," I recommend that you reread MD&TS for September a year ago and also the December issue. Wing loading is a lousy way to compare models with each other and with full-scale airplanes, because wing loading varies with the size of the plane. The problem is that we are dividing weight, a cubic-like function (weight is proportional to volume which we measure in cubic feet) by area, a squared function measured in square feet. We should be, and many modelers are, comparing planes by their wing cube loading, which is independent of size because both the numerator and the denominator are cubic.
     As an example, the cube loading of a scale-weight, quarter-scale Piper Cub and a scale-weight .049-powered Piper Cub model will have exactly the same wing cube loading as each other and as a full-scale Piper Cub. This way we can compare airplanes directly and get a much better picture of how we are doing as model builders. The plain wing loading of these three Cubs would be very different from each other due to the size differences, and quite useless in comparing the planes. Even worse is the fact that we tend to forget that wing loading varies with size, and wonder why the quarter-scale model has a much higher wing loading than the small model. We didn't build it too heavy; we used the wrong measure of comparison.
     Area is a squared term because it consists of a linear term (span) times another linear term (chord). We can change wing area to a cubic term by multiplying it by the square root of wing area, another linear term. Are some of you lost? Sorry; tried. You may note that in my original effort last September, I didn't use square root of area for the third linear term, and the result wasn't independent of aspect ratio. When we introduce the square root of wing area, as proposed to me by reader William Kuhnle, the relationship is dependent only on the size-to-weight ratio. So don't use the formulas and examples in the September issue, use these instead.
     Wing Cube Loading equals the weight of the airplane in ounces divided by the wing area in square feet and divided by the square root of wing area. The units of wing cube loading are weight per unit volume the same as density. This makes sense, since both cube loading and density are measures of relative weight.
     These days one can get a pocket calculator with a square root key for ten dollars, or you can use the curve in Figure 1 to simplify calculating wing cube loading for a large range of model wing areas. You will note that the curve is for area to the 1.5 power, which is of course the 3/2 power, or area times the square root of area. I'm such a helpful guy that I also put square feet on the chart as well as square inches, to save you the trouble of dividing by 144. So to get WCL, in lieu of a square root table or calculator, take the weight of the plane in ounces and divide it by its wing area to the 1.5 power as read from the curve. WCL= W/(S to the 1.5 power).

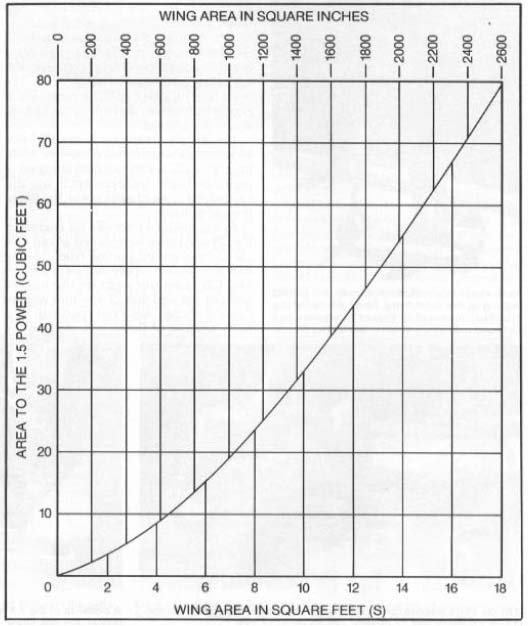
Figure 1

     I said earlier that the WCL of a scale model of scale weight will be the same as that of its full-scale prototype. That is true, but most actual scale models have wing cube loadings on the order of a third lower than their prototypes, because we commonly build our scale models lighter than scale weight. The reason is that we wouldn't like the way scale-weight models fly. They would have to fly a bit fast for our human reflexes, especially old reflexes like mine. If scale event rules required scale weight as well as scale dimensions, the flight part of the event would suffer greatly. So model WCLs are a little lower than full scale WCLs, but model wing loadings are many times lower than full scale WLs.

     True or mathematically correct velocity scaling requires that the model fly at the prototype speed divided by the square root of the scale factor. Quarter-scale models should therefore theoretically fly half as fast as their prototypes, and one sixth scale models should fly 41% as fast. However, I understand that scale judges sometimes grade down a scale model whose flight is too fast to "look scale." Actually, as we usually build lighter than scale weight, most of these scale models are able to fly at a lower scale speed than their prototypes, but "apparent" scale speed differs from true scale speed.
     Will Kuhnle points out to me that for models to fly at apparent or "visual" scale speed (prototype speed divided by scale factor), their weights should be proto weight divided by the fourth power of the scale factor. Wing Quad Loading anyone? Sometimes I wish I had never gotten involved in all of this!

     A year ago I mentioned that others had also proposed similar solutions to the wing loading problem. Only when the letters came in after my cube-loading column was published did I realize how many others, and how long this effort has been going on. Others have called it cube loading, wing volume loading, density factor, flyability factor, volumetric loading, etc. Some of the proposals were identical to what I am now preaching, but they sometimes used different names and different units. To give credit where credit is due, these are the people I know of who have been significantly involved. Bob and Roland Boucher, Chuck Cunningham, John McMasters, Ted Off, Dave Platt, Larry Renger, Ken Runestrand, Tom Stark, Ron St. Jean, Joe Wagner, Kent Walters, R.H. Warring (in England), and Nelson Whitman.
     Several of the above took a wrong turn, in my opinion, when they proposed wing thickness as the third linear term to make a wing volumetric loading. One argued that a thick wing will generate more lift than a thin wing, and a thick wing would and "should" (?) result in a lower cube loading number, to reflect a "superior" airplane. High aspect ratio also indicates a superior airplane, so it could also be used, just as logically, for the third dimension. However, I am not hunting for a number that rolls all the reasons for aerodynamic superiority into one. Instead, I and others of the above want a pure weight-to-size ratio measurement, which is independent of scale. WCL, as proposed, fills that bill exactly.

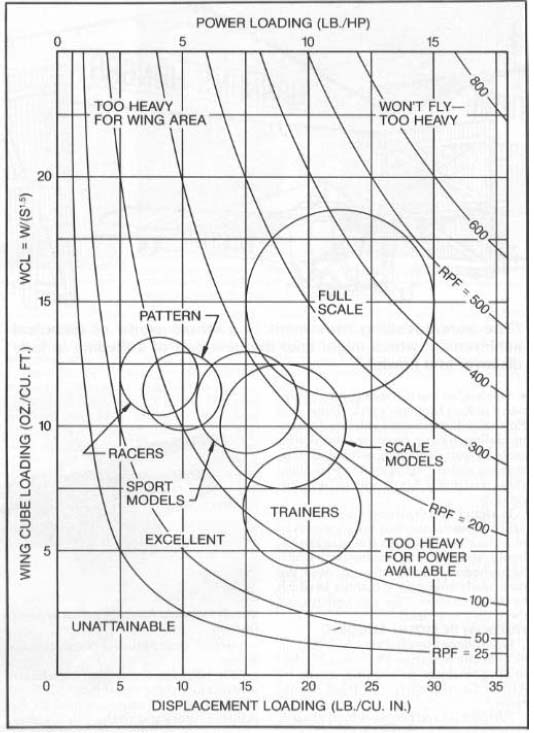
Important Note: December 2021 - Larry Renger uses span, in inches, times the wing area, in square inches, as the multiplier to create a cubic volume in his article "3D Wing Loadings" in the December 1997 issue of Model Airplane News. KM

     Modelers have a mess with regard to units, even before we talk about cube loading. We measure in inches and feet while the rest of the world uses centimeters. We talk about square inches of wing area until we calculate wing loading, then we change to square feet. Most modelers seem to weigh their models in ounces. I weigh mine in grams on a metric balance and convert the grams to pounds, which is the unit I think in. Then I have to convert the pounds to ounces to calculate wing loading in the usual units. Many different units are possible for our cube, volumetric or density loading parameter. After much thought, I have decided to use ounces and feet in calculating WCL, as these are the units commonly used for wing loading, and the answers come out as small easy-to-remember numbers.

     In the mid 1970s, Nelson Whitman compiled a list of the WCLs on over eighty published models. I can't publish Nelson's list but I can summarize it, with some shifts to account for changes in design in 14 years. The WCL for gliders will average around 4, R/C Trainers around 6, Sport Aerobatic ships about 9, Pattern jobs about 11, R/C Racers around 12, Scale Models from 10 to 15, and Full-scale Airplanes 15 to 20.

     I put "average" in italics above because you will find a great range of WCLs for all types of models. WCL will depend on the design, the materials, and the builder, but not the size. I didn't include the range of numbers that Nelson arrived at from his data, because they are too variable, and there will always be some unusual airplanes outside the normal range. The question, "What is normal?" applies.

     Our goal, for any model, should be the lowest possible weight consistent with adequate power, strength and stiffness. If you have forgotten the thirteen reasons why light models are better than heavy models reread MD&TS for October 1988. You say you like to fly fast and hot, so you want a heavy model. Wrong thinking. A model may fly fast in spite of being heavy, if it has lots of power. If you lighten it, it will fly still faster (because there will be less induced drag); and it can also fly slower. Reducing the weight of a model reduces both its wing loading and its power loading, so there is a double-barreled gain.
     In response to my request of last year for cube loading data on different models, I heard from many of you. Thank you all. I decided not to publish your data in detail, because of lack of space and because few individual models would be of interest to the majority of readers. I have used your contributions in making the graph of Figure 2. However, before we discuss that, we should talk about power loading, displacement loading, and performance factor, as these are also part of that graph.

     Not only do we need to build our models light, but we must build in enough power to fly them the way we want them to fly. Power loading or displacement loading figures help us in deciding how much power we need, or why an existing plane flies the way it does. Displacement Loading (DL) is the weight of the airplane (this time in pounds, to keep the numbers nice) divided by the displacement of the engine in cubic inches. For reasons we discussed a year ago, we can equate our various types of power plants to each other and to full scale as follows: Power loading in pounds per horsepower will be roughly twice our displacement loadings. In other words, our modern two-stroke glow engines average about two horsepower per cubic inch of displacement. The disp. loading or DL of models powered by Schnuerle-ported glow engines and Davis Diesel conversions are simply pounds divided by cubic inches. For older non-Schnuerle glow engines multiply the disp. loading by 1.25. For Quadra-type gasoline engines and for four-stroke glow engines, multiply by 1.5. For antique Diesel engines, multiply by 1.75, and for antique spark ignition model engines, multiply by 2.0. Those of you with engines specified in cubic centimeters can convert the displacement to cu. in. by dividing by 16.4.

     I received a lot of good help from Roland Boucher, Mitch Poling, and Nelson Whitman on getting power-loading information for electric-powered models. Electric power seems simple compared to internal combustion, but it is not. For one thing, we can get a huge range of power out of any particular electric motor and prop combination by supplying it with a range of voltages (using batteries with different numbers of cells). If you have an ammeter and a voltmeter, you can measure the input watts to the motor while it is driving the prop (watts = amps X volts). Multiply watts by a motor efficiency of 70 or 75% and divide by 746 to again get approximate output horsepower. This approach will be more accurate than the equivalent-displacement designations given to many model electric motors, because the latter can be valid for only one specific battery and prop.
     Another approach to measuring the power of electrics or any type of power plant is to calculate the power absorbed by the propeller, which of course must equal the output of the engine. I am told that a formula for this purpose was published in one of the mags about a year ago. As the formula was passed on to me, however, it doesn't work for all sizes of props, and doesn't agree with the formulas in my aerodynamics books. Can anyone help us? I don't have back issues of all the model magazines; so if you have it, please send me a copy of the article with the formula for horsepower absorbed by a propeller.

     Rubber-powered models may be compared by relationships proposed to me by reader Barney Frommer. He points out that the potential energy of a rubber motor is proportional to the volume of rubber used. That volume, of course, equals the length of the motor times its cross-sectional area. Barney notes that the duration of the motor run is determined by the length, and the power is determined by the cross section of the rubber (and the prop). Unfortunately, cross sectional area is a square term, and we need a cube term for our power relationship. Otherwise the power loading numbers would vary with scale, as wing loading does. Barney proposes we do what we did to convert wing area to a cube for wing cube loading; multiply the rubber cross section by its square root. Beautiful! Now power loading for rubber powered equals weight of the model divided by the cross sectional area of the rubber motor to the 1.5 power. The units of Rubber Cube Loading are pounds per cubic inch, the same as for displacement loading. Quite by chance the numbers for RCL come out close to DL numbers, but a little lower. For a rough conversion from RCL to DL, multiply the RCL by 1.17. Thanks for the good work, Barney.
     The propeller horsepower formula, when we get it right, will also be applicable to rubber power. The special shape of rubber-power props may require a different constant in the formula however.

     How do you want it to fly? For a scale model of an early antique design, to fly only like the original did, you can use the same high power loading or displacement loading the prototype had, which may be a DL of 25 pounds per cubic inch or more. Make sure this is what you really want, though. It will climb very little, may have trouble making moderate level turns without snap rolling, and may descend if you use anything but full throttle. As with WCL, the displacement loading or power loading of a scale model will usually be somewhat lower than the DL or PL of its prototype, again because we like more performance than we would get from a model with scale power, and we lose some efficiency due to the low Reynolds numbers of models.
     If you want to fly your model straight up and accelerate while doing it, you will need more thrust than the weight of the plane, which means a very low displacement loading. Thrust also depends on propeller size, pitch, and efficiency, but with our modern model props and a good unpiped engine, the displacement loading required for sustained vertical flight appears to be about 10 pounds per cubic inch or less. In other words, if you have a hot forty in a four-pound model, a sixty in a six pounder or a ninety in a nine pounder, you will usually have plenty of "vertical performance.

     Wing cube loading and displacement loading figures each tell us something about a model, but taken together, they give us a more complete picture of a model's potential. For instance, an airplane with a high wing cube loading may still be a very good racing plane, if it has a very low power loading. Likewise, a plane with a high power or displacement loading but a low wing cube loading may still be a fine special-purpose machine such as a scale Jenny or a motor assisted sailplane.
     Some previous writers, including Stinton, in his book, The Design of the Airplane, have proposed performance factors, which combined wing loading and power loading, but these had the same size dependency that we have observed in wing loading itself. Therefore, let's use wing cube loading, and have a performance factor, which is independent of size.
     I call my combined factor "Reynolds Performance Factor." RPF = WCL x 8882 DL. The units of RPF will therefore be ounces per cubic foot and pounds per cubic inch. Sounds messy, but don't worry about the units, just use it. Wing loading and wing cube loading are really indicators of landing or stall speed, while power loading and displacement loading are indicators of maximum speed potential as well as rate of climb. Therefore one times the other or RPF is an indicator of speed range. Normally we consider a big speed range as highly desirable. The lower the RPF the greater the speed range and the better the airplane.

     If we multiply a very low WCL of six by a very low DL of six, we get a very high- performance model (if it will stay together), with an RPF of only thirty-six. Probably this is too light to be practical. At the other end of the range, a heavy underpowered plane with a WCL of fifteen and a DL of twenty would have an RPF of three hundred. It won't be much of a flier, if it flies.
     To get a better picture of the usefulness of RPFs, study Figure 2. This is a corrected and updated version of the chart in last September's column. The curves are lines of constant Reynolds performance factor as labeled, so you can estimate the RPF of any plane without multiplying. I have included circles to show the general areas where different types of airplanes will fall.
     These circles should apply regardless of the type of power used, including electric and rubber, if the power conversion factors, which have been proposed, are accurate. I don't guarantee the circles are in just the right places, or the right size to include most of the good airplanes of each type. They are only SWAGS (scientific wild-assed guesses).
     Calculate the WCLs and the DLs for your models and any other planes you are interested in and plot their points on the Figure. If you prefer a little more space or don't want to mark up your magazine, I will mail you an 8-1/2 x 11 copy of the original for a dime and a self-addressed stamped envelope (two dimes if you want Fig. 1 also).
     Performance factors have been presented in many forms, and the subject is somewhat controversial. Fellow engineer/ experienced modeler; William Kuhnle (who helped me with the math and the logic of it all) proposed some. So did another engineer/model designer, Denis Mrozinski. I have studied these and others, and still prefer RPF. Anyway, this is my column!
     Regular use of these design tools will make you a better model designer, and even a better kit or ARF buyer. Learn to think in terms of and use wing cube loading and displacement loading, but beware! There are myriad reasons why an airplane can be poor. These numbers are only intended to show that a model is light enough and has enough power to be a good airplane if it is otherwise a good design.
     I am sorry if much of the above is more technical than some of you prefer. I feel it needed to be discussed, and I don't know how to do that adequately in simpler words. On the other hand I apologize for boring those of you who are way ahead of me.

When we learn by experience, we never get out of school.
Francis Reynolds, 3060 W. Lk Sammamish Pkwy. N., Redmond, Washington 98052.